The Perdikaris Group has a new paper in preprint about deep operator networks.
Abstract
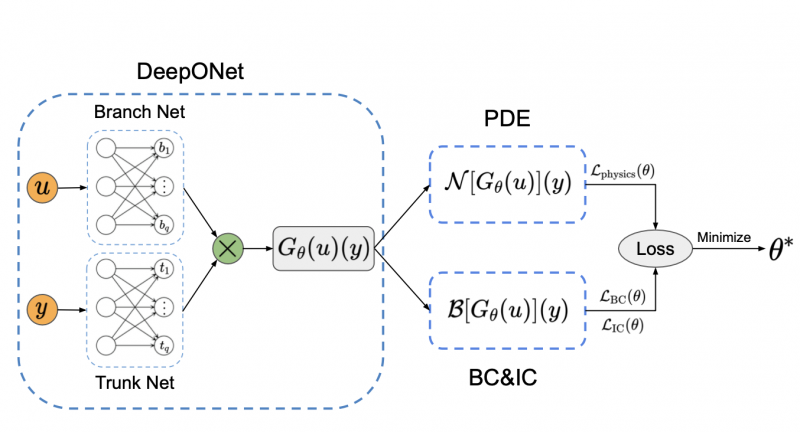
Deep operator networks (DeepONets) are receiving increased attention thanks to their demonstrated capability to approximate nonlinear operators between infinite-dimensional Banach spaces. However, despite their remarkable early promise, they typically require large training data-sets consisting of paired input-output observations which may be expensive to obtain, while their predictions may not be consistent with the underlying physical principles that generated the observed data. In this work, we propose a novel model class coined as physics-informed DeepONets, which introduces an effective regularization mechanism for biasing the outputs of DeepOnet models towards ensuring physical consistency. This is accomplished by leveraging automatic differentiation to impose the underlying physical laws via soft penalty constraints during model training. We demonstrate that this simple, yet remarkably effective extension can not only yield a significant improvement in the predictive accuracy of DeepOnets, but also greatly reduce the need for large training data-sets. To this end, a striking observation is that physics-informed DeepONets are capable of solving parametric partial differential equations (PDEs) without any supervision, except for a set of given initial or boundary conditions. We illustrate the effectiveness of the proposed framework through a series of comprehensive numerical studies across various types of PDEs. Strikingly, a trained physics informed DeepOnet model can predict the solution of $\mathcal{O}(10^3)$ time-dependent PDEs in a fraction of a second — up to three orders of magnitude faster compared a conventional PDE solver.